Обсуждаются вопросы создания моделей социально-исторических процессов. Показано, что основное внимание должно уделяться моделированию самоорганизации и эволюции рассматриваемых социальных систем. Обсуждаются общие принципы моделирования в истории. Изложенные подходы использовались при создании ряда моделей, отражающих закономерности социально-исторической динамики в обществах различного типа. Логико-математическое моделирование социально-исторических процессов является сложной задачей. Это обусловлено слабой формализуемостью многих понятий и факторов социальной эволюции, многофакторностью, динамичностью, неустойчивостью протекающих процессов, необходимостью учета множественных рефлексивных связей при взаимодействии социальных субъектов. Тем не менее, в последние годы, на основе достижений синергетики и компьютерных технологий, достигнуты значительные успехи в области создания моделей подобного типа [1]. Имеющиеся к настоящему времени модели социально-исторических процессов можно условно разделить на три группы: 1) модели-концепции, основанные на выявлении и анализе общих исторических закономерностей и представлении их в виде когнитивных схем, описывающих логические связи между различными факторами, влияющими на исторические процессы (Дж. Голдстайн, И. Валлерстайн, Н. Гумилев, Н. Розов и др.). Такие модели обладают высокой степенью обобщения, но имеют не математический, а чисто логический, концептуальный характер; 2) частные математические модели имитационного типа, посвященные описанию конкретных исторических событий (Ю. Павловский, Л. Бородкин, Д. Медоуз, Дж. Форрестер и др.). В подобных моделях основное внимание уделяется тщательному учету и описанию факторов и процессов, оказывающих влияние на рассматриваемые явления. Недостаток таких моделей — ограниченная узким пространственно-временным интервалом применимость. Они «привязаны» к конкретному историческому событию и их невозможно интерполировать на протяженные периоды времени; 3) математические модели, являющиеся промежуточными между двумя указанными типами. Эти модели описывают некоторый класс социальных процессов без претензии на детальное описание особенностей для каждого конкретно-исторического случая. Их задачей является выявление базовых закономерностей, характеризующих протекание процессов рассматриваемого вида. В соответствии с этим данные математические модели называются базовыми. С точки зрения моделирования тенденций и направленности социальной эволюции, анализа причин и последствий тех или иных исторических событий наибольший интерес представляют базовые модели. Основой создания таких моделей является математическое описание процессов социальной самоорганизации и эволюции с учетом сложившихся конкретно-исторических условий в рассматриваемом географическом регионе. Общими свойствами социальных систем (СС), которые необходимо учитывать при моделировании, являются следующие:
Наличие данных свойств является причиной возникновения следующих особенностей самоорганизации и эволюции социальных систем. 1. Нелинейный характер взаимодействия субъектов и ограниченность ресурсов определяют специфику динамических процессов в социальных системах: диалектику развития отражает не формула «тезис – антитезис – синтез», а формула «тезис – антитезис – временный компромисс». Возникающие в процессе эволюции социальных систем временные компромиссы зависят от внешних условий и имеющихся ресурсных ограничений. Когда последние изменяются, динамическое равновесие нарушается, начинается новая борьба субъектов с выходом на новый компромиссный уровень. 2. Общий принцип социальной динамики: хаос на микроуровне – порядок на макроуровне. Пробуется в социальной практике все, что возможно (не запрещено какими-либо объективными законами), но закрепляется в виде социальных структур только то, что устойчиво к внешним и внутренним дестабилизирующим процессам и воздействиям. 3. Устойчивость развития конкретной социальной системы (необходимая для ее социально-политического «выживания») при наличии перманентных противоречий между ее элементами достигается путем проб и ошибок. В результате вырабатываются механизмы компенсации внутренних напряжений в СС. К таким механизмам относятся:
Те социальные системы, которым удается выработать эффективную систему компенсации внутренних напряжений, выживают. Те социальные системы, которым это не удается, в конечном счете распадаются или гибнут в конкурентной борьбе с другими системами. Конкретный вид системы компенсаций, обеспечивающий устойчивость рассматриваемого общества, характеризует его социокультурную специфику и отличие от других обществ.
4. Для социальных систем характерна возможность многовариантного развития, обусловленная тем, что имеется, как правило, не одно, а несколько квазиустойчивых состояний (аттракторов) при заданных внешних условиях. Эта ситуация отражена на рис.1. На нем в пространстве координат, характеризующих состояние социальной системы, изображены возможные траектории ее эволюции, обусловленные процессами социальной самоорганизации. Точки А1 и А2 на рисунке – аттракторы типа «центр», к которым стремится система в результате своей эволюции; области G1 и G2 – области притяжения аттракторов. Система под воздействием процессов самоорганизации через некоторое время окажется в одном из аттракторов (это свойство называется эквифинальностью), однако в котором из них – зависит от многих факторов, в том числе, и от предыстории развития социальной системы (историческая и культурная память), и от целенаправленной деятельности ее органа управления (правительства). Таким образом, пути развития социальных систем не произвольны. Надо знать законы самоорганизации и использовать их для того, чтобы система в конечном итоге оказалась в наиболее благоприятном аттракторе. В этом заключается основная задача государственного управления. 5. Возможны как эволюционный, так и революционный (через кризисы) типы развития социальных систем.
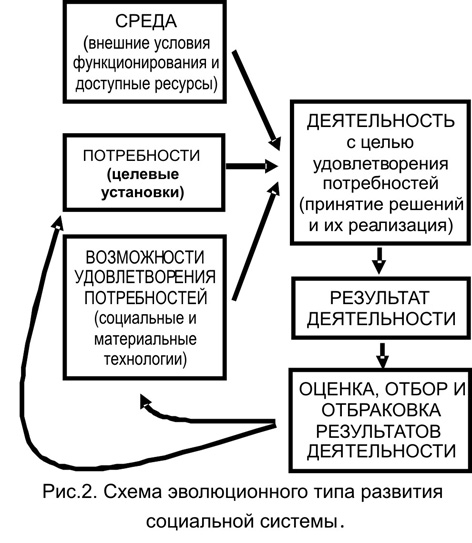
Эволюционный процесс (рис.2) основан на способности социальных систем к адаптации к условиям внешней среды путем вариации способов функционирования. Вариации имеют, как правило, случайный характер (перебор возможных вариантов развития), и большая часть из них выбраковывается в результате взаимодействия со средой. Факторами отбраковки для экономических субъектов является конкуренция в рыночной среде, для государственных образований – межгосударственная борьба. Выживает более приспособленный и более устойчивый к внешним дестабилизирующим воздействиям. Стратегии выживания затем закрепляются через нормы морали, законы, социальные институты и т.п.
Схема развития революционного типа (развития через кризисы) представлена на рис.3. Суть «развития через кризисы» заключается в том, что социальные системы в процессе адаптации к внешней среде имеют тенденцию к усложнению своей организации, что обеспечивает им более высокий уровень специализации в использовании имеющейся ресурсной базы. В процессе функционирования (жизнедеятельности) системы влияют на окружающую среду и изменяют ее. В результате накопившихся изменений сложившаяся организация системы перестает соответствовать новым внешним условиям и возникает кризис, который может закончиться дестабилизацией и распадом системы. Наиболее уязвимы в кризисных условиях, как правило, верхние уровни организационной иерархии, поскольку они являются наиболее специализированной частью системы. Здесь возможны два исхода. В первом случае верхним уровням иерархии в результате целенаправленных усилий удается переорганизовать (реформировать) систему и сделать ее более адекватной изменившимся внешним условиям. Это «реформаторский» сценарий развития кризисной ситуации без необратимого разрушения системы. Во втором случае адаптационных возможностей системы оказывается недостаточно, и кризис приводит к ее распаду, сопровождающемуся архаизацией и уничтожением специализированных верхних уровней ее организационной иерархии. Дальнейшая эволюция идет по пути самоорганизации способов функционирования новой системы, осознанно или неосознанно использующей при своем формировании отдельные патерны генетической памяти о судьбе своей предшественницы. Это «катастрофичный» сценарий развития, приводящий к наиболее резким изменениям системы. Изложенные подходы использовались при создании ряда моделей, отражающих закономерности социально-исторической динамики [2 - 15]. Полученные результаты позволяют с оптимизмом оценивать возможности логико-математического моделирования социальной эволюции и исторических процессов. Работа поддержана РФФИ (проект №01-06-80142) ЛИТЕРАТУРА 1. Плотинский Ю.М. Модели социальных процессов: Учебное пособие для высших учебных заведений. – М.: Логос, 2001 2. Малков С.Ю. К вопросу об историометрических циклах // Вестник РАН, 1997, т.67, №8, с.707-711. 3. Малков С.Ю. Математическое моделирование социально-экономических процессов. Подходы и решения // Стратегическая стабильность, 1998, №1, с.62-67. 4. Малков С.Ю. Использование методов исследования устойчивости сложных систем для анализа условий стабильного развития стран европейского региона // Стратегическая стабильность, 1998, №2, с.81-92. 5. Малков С.Ю. Политика с точки зрения синергетики // Стратегическая стабильность, 1998, №3, с.90-99. 6. Малков С.Ю., Ковалев В.И., Коссе Ю.В., Малков А.С. Математическое моделирование социально-экономических процессов. Применение моделей к анализу перспектив российских реформ // Стратегическая стабильность, 1999, №1, с.34-46. 7. Малков С.Ю., Ковалев В.И., Коссе Ю.В., Малков А.С. Российские модернизации последнего столетия в свете математического моделирования // Технико-экономическая динамика России: техника, экономика, промышленная политика. М.: ГЕО-Планета, 2000, с.215-238. 8. Малков С.Ю. Динамика общественной жизни и Солнце //Технико-экономическая динамика России: техника, экономика, промышленная политика. М.: ГЕО-Планета, 2000, с.164-175. 9. Малков С.Ю., Ковалев В.И., Малков А.С. История человечества и стабильность (опыт математического моделирования) // Стратегическая стабильность, 2000, №3, с.52-66 10. Малков С.Ю., Малков А.С. Математические методы в исследовании закономерностей развития общества: моделирование эволюции этнических систем // Стратегическая стабильность, 2000, №4, с.31-36. 11. Малков С.Ю., Малков А.С. История в свете математического моделирования // История за и против истории, книга 2.- М.: Центр общественных наук, 2000, с.54-76. 12. Малков С.Ю. Математическое моделирование исторических процессов // Новое в синергетике. Взгляд в третье тысячелетие / Под ред. Г.Г.Малинецкого, С.П.Курдюмова. - М.: Наука, 2002. 13. Малков С.Ю., Коссе Ю.В., Бакулин В.Н., Сергеев А.В. Социально-экономическая и демографическая динамика в аграрных обществах // Математическое моделирование, 2002, т.14, №9, с.103-108. 14. Чернавский Д.С., Чернавская Н.М., Малков С.Ю., Малков А.С. Математическое моделирование геополитических процессов //Стра¬тегическая стабильность, 2002, №1, с.60-66. 15. Малков С.Ю., Сергеев А.В. Математическое моделирование социально-экономической ус-тойчивости развивающегося общества //Стра-тегическая стабильность, 2002, №4, с.54-61 |
||||||||||||||